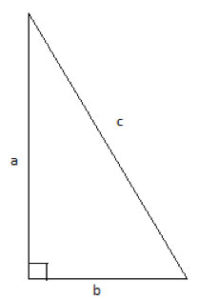
Triangles

A triangle is one of the most basic shapes in geometry- and object with three straight sides (“edges”) and three angles, formed where each of the two sides meet. These meeting points are called “vertices”.

Triangle Notation

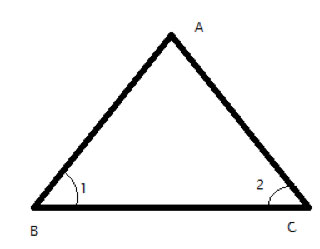
A triangle is often noted by using the points at its vertices, for example: ΔABC

And the angles in the triangle are often defined by the points, as well, so ∠1 can be written as ∠ABC and angle ∠2 can be written as ∠ACB. The vertices where the angle is the middle letter in this type of notation.

Basic properties of triangles

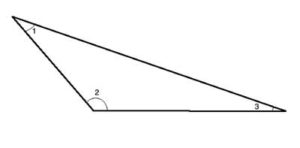
One of the basic properties of triangles is that the sum of the measure of angles, in every triangle, is 180°, as we will now prove, using what we know about parallel lines and the angles formed by a transversal line.

Proof: The sum of the angles in a triangle is 180°.

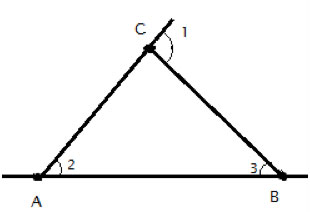
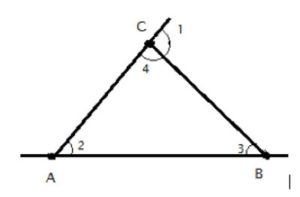
If we extend the triangle’s sides beyond the triangle, we form angles between the line’s extension and the angle inside the triangle, like angle1 below. These angles are called ”exterior angles”:

Having just proven that the sum of the angles in a triangle is 180°, it is now simple to prove a corollary theorem, that the measure of an exterior angle at a vertex of a triangle is equal to the sum of the measures of the interior angles at the other two vertices of the triangle (called the remote interior angles). Proof: The exterior angle is equal to the sum of the two remote interior angles

--
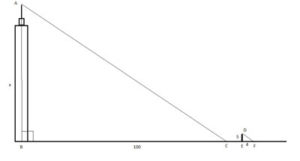
Now that we've explained the basic concept of triangles in geometry, let's scroll down to work on specific geometry problems relating to this topic.